Source: 

In bridge, the Law of Total Tricks (or simply “The Law”) is a hand evaluation method for competitive auctions. Technically stated, the total number of cards in each partnership’s longest suit is equal to the number of “total tricks” that either side can win in a suit contract.

This is pretty wordy, so I think it’s best to jump into some examples…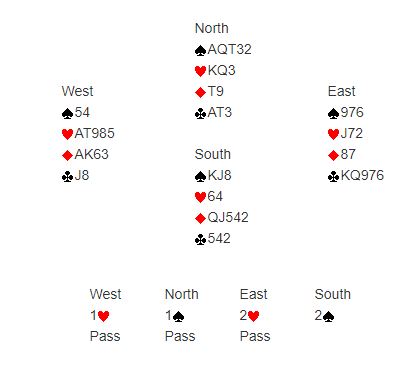

This is a typical Law deal. East-West have 8 hearts and North-South have 8 spades. 8 hearts + 8 spades = 16 total trumps. That number happens to be the combined number of tricks that can be made in 2and 2. Playing 2, West would make exactly 8 tricks after losing 2 spades, 2 hearts and a club. In 2, North would also win 8 tricks against best defense, losing a heart, 2 diamonds and 2 clubs. 8 heart tricks + 8 spade tricks = 16 “total tricks”.

The principle is the same if we move some cards around:

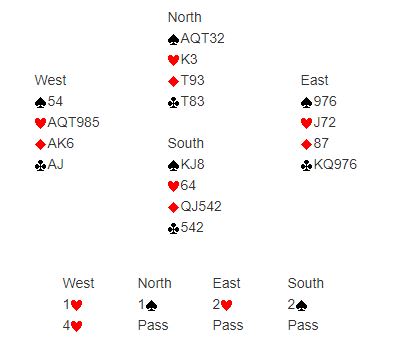
North-South still own an 8-card spade fit, but East-West now enjoy a 9-card heart fit. 8 spades + 9 hearts = 17. Playing 4, West will win 11 tricks against best defense, losing only 2 spades. If North were allowed to play 2, he would only win 6 tricks; East-West would score 2 diamonds, a diamond ruff, 3 clubs and a heart. 11 tricks + 6 tricks = 17, which is equal to the total number of spades and hearts in the deal.

The bidding in the above examples was clear-cut, with or without the Law. So let’s look at a hand in which the Law may actually influence the bidding. Sitting East, you hold:

 973    KQ32    J2   QT72
The auction begins:

1. 5-card major.

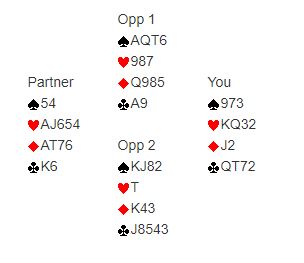Playing a natural 5-card major system, you have already described your hand with 2, and it may seem obvious to pass. But the Law would actually suggest bidding 3. The full deal:The opponents hold 8 spades, while your side holds 9 hearts. 8 + 9 = 17, so the Law says there should be 17 total tricks available. Therefore, if the opponents can make 2 (8 tricks), then your side can make 3 (9 tricks). That is the case in this deal.

This leads to the most important application of the Law…

In my experience, this is most common and critical at the 2- and 3-levels. If you and your partner have an 8-card fit, then you are usually safe to compete to the 2-level in that suit. And if you own a 9-card fit, then you’re usually safe to compete to the 3-level. The contract will either make, or be a good sacrifice against whatever the opponents can make.

1. Corollary: Get to the right level quickly. In the above auction, East bid 2 first, which allowed the opponents to compete in spades. Playing Bergen raises, a bidding convention based on the Law, East could have shown 4-card support immediately. Moreover, Bergen raises allow a major-suit jump raise (i.e. 1 – 3) with 0 points, because of the Law’s premise of a 9-card fit. This is something that standard bidding methods would never allow.
2. Corollary: Do not compete above your trump fit unless you have extra shape, points, or vulnerability in your favor. For example, South could bid 3 over 3 in the above auction. However, this is much more attractive if North-South are not vulnerable. If vulnerable, 3doubled is -200 which is obviously a worse score than defending 3.
3. Corollary: There are “adjustments” to the Law to consider when bidding. I am not a big fan of this, and consider it to be the major weakness of the Law. Depending on the distribution of the cards, sometimes the number of total trumps does NOT equal the number of total tricks. The Law is sometimes incorrect depending on how strong each side’s trump holding are, and how many total trumps exist. Once a deal gets above 18 total trumps, the Law can be a little erratic. For example:20 total trumps in hearts and spades but only 18 total tricks. 4 is cold for East-West, but North-South can only make 2. Depending on the vulnerability, it may be correct for North-South to sacrifice in 4 – the 10 combined trumps recommends it. But clearly, something is amiss with the Law here.

   Origins

   The Law of Total Tricks was originally proposed by Jean-René Vernes in his 1966 book “Bridge Moderne de la Défense.” He subsequently wrote a synopsis of the Law in a Bridge World article circa June 1969. More recently it has been popularized by American experts Marty Bergen and Larry Cohen. Cohen is the author of the title “To Bid or Not to Bid: The Law of Total Tricks.”